오늘의 문제 - 힙
문제 설명
매운 것을 좋아하는 Leo는 모든 음식의 스코빌 지수를 K 이상으로 만들고 싶습니다. 모든 음식의 스코빌 지수를 K 이상으로 만들기 위해 Leo는 스코빌 지수가 가장 낮은 두 개의 음식을 아래와 같이 특별한 방법으로 섞어 새로운 음식을 만듭니다.
섞은 음식의 스코빌 지수 = 가장 맵지 않은 음식의 스코빌 지수 + (두 번째로 맵지 않은 음식의 스코빌 지수 * 2)
Leo는 모든 음식의 스코빌 지수가 K 이상이 될 때까지 반복하여 섞습니다.
Leo가 가진 음식의 스코빌 지수를 담은 배열 scoville과 원하는 스코빌 지수 K가 주어질 때, 모든 음식의 스코빌 지수를 K 이상으로 만들기 위해 섞어야 하는 최소 횟수를 return 하도록 solution 함수를 작성해주세요.
제한 사항
- scoville의 길이는 2 이상 1,000,000 이하입니다.
- K는 0 이상 1,000,000,000 이하입니다.
- scoville의 원소는 각각 0 이상 1,000,000 이하입니다.
- 모든 음식의 스코빌 지수를 K 이상으로 만들 수 없는 경우에는 -1을 return 합니다.
입출력 예
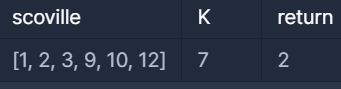
내 풀이 및 접근 방식
힙을 쓰지 않고 풀이를 해보았는데 역시나 시간 초과
def solution(scoville, K):
answer = 0
scoville.sort()
while scoville[0] < K and len(scoville) >= 2:
scoville[1] = scoville[0] + scoville[1]*2
scoville = scoville[1:]
scoville.sort()
answer += 1
if scoville[0] >= K:
return answer
else:
return -1
시간복잡도
- 초기 정렬: O(nlogn)
- 반복문: O(n^2log n)
슬라이싱 O(n), 정렬에서 O(nlogn)
반복될 때마다 하나의 요소가 지워지므로, 최악의 경우 n번 반복 O(n)
O(n) * O(nlogn) = O(n^2logn)
다른 풀이
힙 이용 풀이
import heapq
def solution(scoville, K):
answer = 0
heapq.heapify(scoville)
while len(scoville) >= 2:
min_1 = heapq.heappop(scoville)
# 최솟값이 K 이상인 경우
if min_1 >= K:
return answer
else:
min_2 = heapq.heappop(scoville)
heapq.heappush(scoville, min_1+min_2*2)
answer += 1
if scoville[0] >= K:
return answer
else:
return -1
시간 복잡도
- 힙 초기화: heapq.heapify 함수는 리스트를 힙 구조로 변환하는 작업 수행 => O(n)
- 반복문 => O(nlogn)
heappop 연산을 통해 최솟값 2개 추출 => 2*O(logn) = O(logn)
heappush를 통해 새로운 값 추가 => O(logn)
각 반복에 대한 시간 복잡도는 O(logn)이고, 최악의 경우 n번 반복하므로 시간 복잡도는 O(nlogn)
회고
힙 정리 정리~~
힙(Heap)
완전 트리의 일종으로, 부모 노드가 자식 노드보다 항상 크거나 작아야 하는 성질을 가지고 있는 자료 구조, 우선순위 큐를 구현하는 사용된다. 힙의 종류에는 최소 힙, 최대 힙 2가지가 있다.
- 최소 힙: 부모 노드가 자식 노드보다 작거나 같은 완전 이진 트리, 루트 노드에 가장 작은 값 위치
- 최대 힙: 부모 노드가 자식 노드보다 크거나 같은 완전 이진 트리, 루트 노드에 가장 큰 값 위치
파이썬의 heapq 모듈은 최소 힙을 기본적으로 지원
파이썬에서 힙 주요 합수
- heapq.heapify(iterable): 주어진 iterable을 힙으로 변환, 시간복잡도 O(n)
- heapq.heappop(heap): 힙에서 가장 작은 항목 제거 반환, 시간복잡도 O(logn)
- heapq.heappush(heap, item): 힙에 새로운 항목 추가, 시간복잡도 O(logn)
- heapq.heappushpop(heap, item): 힙에 항목 추가한 후 가장 작은 항목 제거하고 반환, heappush와 heappop 둘다 호출하는 것보다 효율적
- heapq.heapreplace(heap, item): 힙에서 가장 작은 항목 제거하고 새 항목 추가, heappop 후 heappush를 호출하는 것과 동일하지만 더 효율적
최대 힙 구현하기
item에 -1을 곱하여 정렬 후, -1을 다시 곱하여 출력한다.
import heapq
max_heap = []
heapq.heappush(max_heap, -1 * 3)
heapq.heappush(max_heap, -1 * 1)
print([-1 * heapq.heappop(max_heap) for _ in range(len(max_heap))])'코테 스터디 99클럽' 카테고리의 다른 글
| 99클럽 코테 스터디 11일차 TIL + 정렬 (0) | 2024.08.02 |
|---|---|
| 99클럽 코테 스터디 10일차 TIL + 힙 (0) | 2024.08.01 |
| 99클럽 코테 스터디 8일차 TIL + 스택/큐 (0) | 2024.07.30 |
| 99클럽 코테 스터디 7일차 TIL + 스택/큐 (0) | 2024.07.29 |
| 99클럽 코테 스터디 6일차 TIL + 해시 (0) | 2024.07.28 |



