오늘의 문제 - 그래프(Graph)
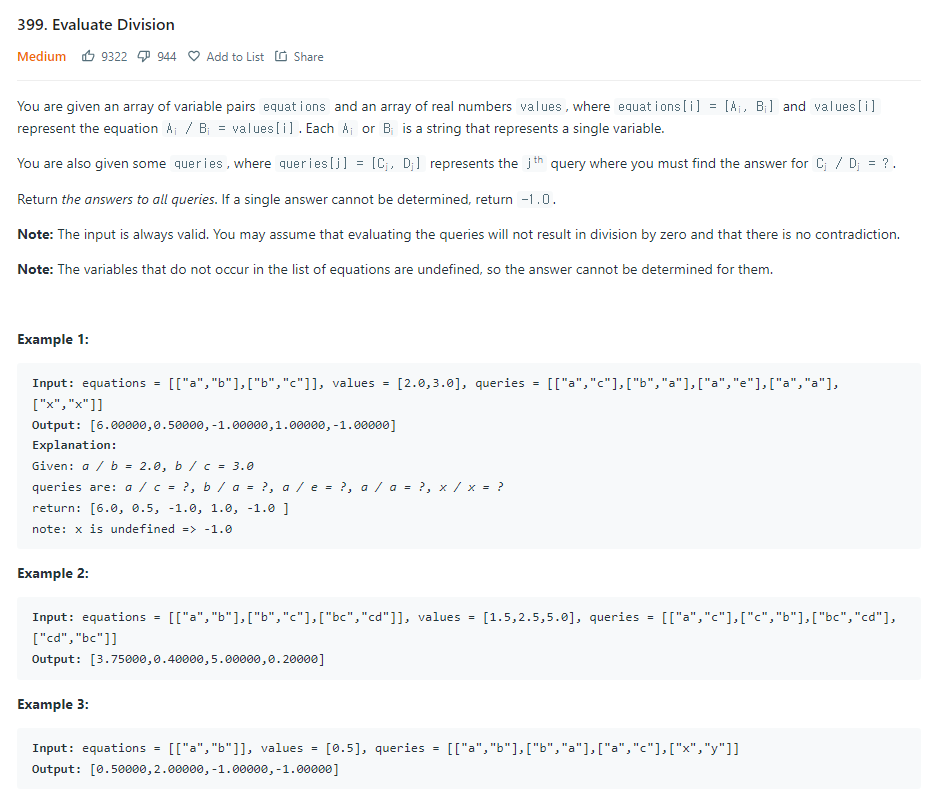
LeetCode - Evaluate Division
https://leetcode.com/problems/evaluate-division/submissions/
내 풀이 및 접근 방식
각 수의 임의값을 구하고 딕셔너리에 저장해서 사용하는 풀이 방식을 생각했다.
class Solution:
def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:
answer = []
nums = {}
# 숫자 임의값 저장
for i in range(len(equations)):
n1, n2 = equations[i]
val = values[i]
if n1 not in nums and n2 not in nums: # 둘 다 사전에 없는 경우
nums[n1] = val
nums[n2] = 1
elif n1 not in nums and n2 in nums: # n1만 사전에 있는 경우
nums[n1] = val*nums[n2]
elif n2 not in nums and n1 in nums: # n2만 사전에 있는 경우
nums[n2] = nums[n1]/val
# 쿼리 결과값 계산
for q in queries:
n3, n4 = q
if n3 not in nums or n4 not in nums:
answer.append(-1)
continue
res = nums[n3] / nums[n4]
answer.append(res)
print(3*A)
return answer
그러나 위 풀이는 잘못된 풀이인데, nums[a] = 3.4, nums[b] = 1, nums[e] = 1.4, nums[f] = 1 이런식으로 저장해버리기 때문에 아래와 같이 잘못된 결과값이 출력된다.

제대로 된 결과값을 출력하기 위해 생각한 방식은 [a,b] 인풋을 계산하면 a나 b가 포함된 리스트를 찾고 그 리스트의 상대적인 수를 구하여 계산하는 것이다. 위 리스트에서 [a,b]에서 nums[a]와 nums[b]의 수를 구하고, [b,e]에 b가 포함되어 있으니 바로 다음으로 nums[b], nums[e]를 구하면 위와 같은 문제를 해결할 수 있을 것이라고 생각했다.
여기서 그래프 알고리즘이 사용되는 것이라고 생각했고, 시간 이슈로 일단 바로 다른 분의 정답 코드를 확인했다.하하
정답 풀이
class Solution:
def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:
# 두 변수간의 관계 그래프 표현
edge = defaultdict(list)
for i in range(len(equations)):
x, y = equations[i]
v = values[i]
# 각 변수는 연결된 변수와 그들 간의 비율 값으로 저장
edge[x].append((y, v))
edge[y].append((x, 1.0 / v))
# 변수들 간의 비율 저장 사전
clusters = []
visit = set()
for x, y in equations:
dic = {}
if x not in visit:
start = x
visit.add(start)
dic[start] = 1
q = [start]
while q:
cur = q.pop()
for n, v in edge[cur]:
if n not in visit:
visit.add(n)
q.append(n)
dic[n] = dic[cur] * v
clusters.append(dic)
# 쿼리 처리
res = []
for x, y in queries:
for cluster in clusters:
if x in cluster and y in cluster:
res.append(cluster[y] / cluster[x])
break
else:
res.append(-1)
return res
# 출처 https://maxming0.github.io/2020/09/27/Evaluate-Division/풀이
- 주어진 equations와 values를 통해 그래프를 구축하고, 이를 통해 서로 관련 있는 변수들 간의 비율을 계산하여 클러스터로 묶는다.
- 각 쿼리에 대해, 두 변수가 동일 클러스터에 존재하는지 확인하고, 존재하면 비율을 계산하여 반환한다. 그렇지 않다면 -1을 반환한다.
회고
그래프와 트리 비교
| 그래프 | 트리 | |
| 방향성 | 방향 그래프 또는 무방향 그래프 | 방향 그래프 |
| 순환성 | 순환 및 비순환 | 비순환 |
| 루트 노드 존재 여부 | 루트 노드가 없음 | 루트 노드가 존재 |
| 노드간 관계성 | 부모와 자식 관계 없음 | 부모와 자식 관계 |
| 모델의 종류 | 네트워크 모델 | 계층 모델 |
그래프 문제 종류는 다양한 것 같아서 접근하기에 어려운 점이 있는 것 같다.
크루스칼 알고리즘 및 위상 정렬 알고리즘도 그래프 유형인데, 크루스칼 알고리즘은 그리디 알고리즘으로, 위상 정렬 알고리즘은 큐 혹 스택으로 구현할 수 있다고 한다.
크루스칼 알고리즘
최소한의 비용으로 신장 트리를 찾아야 할 때 사용하는 알고리즘
ex) n개의 도시 중 a에서 b로 가야할 때 최소한의 비용으로 이동할 수 있는 경로 구하기
- 간선 데이터를 비용에 따라 오름차순 정렬
- 간선을 하나씩 확인하며 현재 간선이 사이클을 발생시키는지 확인
- 사이클이 발생하지 않는 경우 최소 신장 트리에 포함
- 사이클이 발생하는 경우 최소 신장 트리에 포함하지 않음 - 모든 간선에 대하여 위 과정을 반복
위상 정렬
방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것. 순서가 정해져 있는 일련의 작업을 차례대로 수행해야할 때 사용한다.
- 진입차수가 0인 노드를 큐에 넣는다.
- 큐가 빌 때까지 다음의 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
*진입차수 : 특정한 노드로 들어오는 간선의 개수
'코테 스터디 99클럽' 카테고리의 다른 글
| 99클럽 코테 스터디 27일차 TIL + 시뮬레이션 (0) | 2024.08.18 |
|---|---|
| 99클럽 코테 스터디 26일차 TIL + 시뮬레이션 (0) | 2024.08.17 |
| 99클럽 광복절 이벤트 (0) | 2024.08.15 |
| 99클럽 코테 스터디 24일차 TIL + 그래프(Graph) (0) | 2024.08.15 |
| 99클럽 코테 스터디 22일차 TIL + 동적계획법(DP) (0) | 2024.08.13 |



